What is a Radian?

A radian is a unit of measurement defined as 180/π°, or roughly 57.2958°. Sometimes abbreviated as rad or as the subscript c, standing for "circular measure," the radian is the standard unit of measurement for angles in mathematics. The radian was first conceived of by English mathematician Roger Cotes in 1714, though he did not name the unit of measurement. The word radian first appeared in print in 1873.

Originally, the radian was considered a supplementary unit in the International System of Units (SI), but supplementary units were abolished in 1995 and are now known as derived units. The radian is derived from the SI base unit meter (m), being equal to m·m^-1, or m/m. Because the meters cancel each other out in the definition of the radian, the radian is considered dimensionless, and for this reason, radians are often simply written as a number, with no unit symbol.

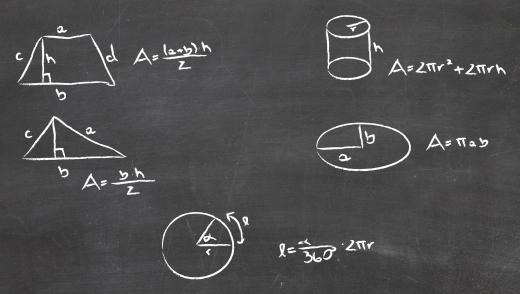
The radian is the angle formed by two radii, lines from the center to the outside circumference of a circle, where the arc formed is equal to the radius. An angle in radians can be calculated by dividing the length of the arc the angle cuts out by the radius of the circle (s/r). There are 360° in every circle, equal to 2π radians. Another system of angles measurement, the grad, divides a circle into 400 grad. 200/π grad is equal to a radian.

In mathematics, radians are preferred to other units of angle measurement, such as degrees and grads, because of their naturalness, or their ability to produce elegant and simple results, particularly in the field of trigonometry. In addition, like all SI units, radians are used universally, so they allow mathematicians and scientists to understand each other's calculations easily without the trouble of conversion.

Another SI derived unit related to the radian is the steradian (sr), or square radian, which measures solid angles. A solid angle can be visualized as a conic portion of a sphere. The steradian is another dimensionless unit of measurement, equal to m·m^-2. Steradians can be calculated by dividing the area covered on the surface of the sphere by the radius squared (S/r²).